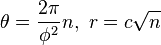9:20 PM Fibonacci number | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Fibonacci numberIn mathematics, the Fibonacci numbers or Fibonacci series or Fibonacci sequence are the numbers in the following integer sequence:[1][2] By definition, the first two numbers in the Fibonacci sequence are 0 and 1, and each subsequent number is the sum of the previous two. In mathematical terms, the sequence Fn of Fibonacci numbers is defined by the recurrence relation with seed values[3] The Fibonacci sequence is named after Leonardo Fibonacci. His 1202 book Liber Abaci introduced the sequence to Western European mathematics,[4] although the sequence had been described earlier in Indian mathematics.[5][6][7] By modern convention, the sequence begins either with F0 = 0 or with F1 = 1. The Liber Abaci began the sequence with F1 = 1, without an initial 0. Fibonacci numbers are closely related to Lucas numbers in that they are a complementary pair of Lucas sequences. They are intimately connected with the golden ratio; for example, the closest rational approximations to the ratio are 2/1, 3/2, 5/3, 8/5, ... . Applications include computer algorithms such as the Fibonacci search technique and the Fibonacci heap data structure, and graphs called Fibonacci cubes used for interconnecting parallel and distributed systems. They also appear in biological settings,[8] such as branching in trees, phyllotaxis (the arrangement of leaves on a stem), the fruit sprouts of a pineapple,[9] the flowering of artichoke, an uncurling fern and the arrangement of a pine cone.[10] ========================================== 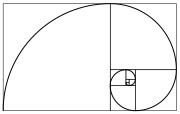
An approximation of the golden spiral
created by drawing circular arcs connecting the opposite corners of
squares in the Fibonacci tiling; this one uses squares of sizes 1, 1, 2,
3, 5, 8, 13, 21, and 34. ====================================================== Origins
A page of Fibonacci's Liber Abaci from the Biblioteca Nazionale di Firenze
showing () labeled in Latin and Roman numerals and the value in
Hindu-Arabic numerals.
The Fibonacci sequence appears in Indian mathematics, in connection with Sanskrit prosody.[6][11] In the Sanskrit oral tradition, there was much emphasis on how long (L) syllables mix with the short (S), and counting the different patterns of L and S within a given fixed length results in the Fibonacci numbers; the number of patterns that are m short syllables long is the Fibonacci number Fm + 1.[7] Susantha Goonatilake writes that the development of the Fibonacci sequence "is attributed in part to Pingala (200 BC), later being associated with Virahanka (c. 700 AD), Gopāla (c. 1135), and Hemachandra (c. 1150)".[5] Parmanand Singh cites Pingala's cryptic formula misrau cha ("the two are mixed") and cites scholars who interpret it in context as saying that the cases for m beats (Fm+1) is obtained by adding a [S] to Fm cases and [L] to the Fm−1 cases. He dates Pingala before 450 BC.[12] However,): The series is also discussed by Gopala (before 1135 AD) and by the Jain scholar Hemachandra (c. 1150). In the West, the Fibonacci sequence first appears in the book Liber Abaci (1202) by Leonardo of Pisa, known as Fibonacci.[4] Fibonacci considers the growth of an idealized (biologically unrealistic) rabbit population, assuming that: a newly born pair of rabbits, one male, one female, are put in a field; rabbits are able to mate at the age of one month so that at the end of its second month a female can produce another pair of rabbits; rabbits never die and a mating pair always produces one new pair (one male, one female) every month from the second month on. The puzzle that Fibonacci posed was: how many pairs will there be in one year?
At the end of the nth month, the number of pairs of rabbits is equal to the number of new pairs (which is the number of pairs in month n − 2) plus the number of pairs alive last month (n − 1). This is the nth Fibonacci number.[14] The name "Fibonacci sequence" was first used by the 19th-century number theorist Édouard Lucas.[15] List of Fibonacci numbersThe first 21 Fibonacci numbers Fn for n = 0, 1, 2, ..., 20 are:[16]
The sequence can also be extended to negative index n using the re-arranged recurrence relation which yields the sequence of "negafibonacci" numbers[17] satisfying Thus the bidirectional sequence is
Occurrences in mathematics
The Fibonacci numbers are the sums of the "shallow" diagonals (shown in red) of Pascal's triangle.
The Fibonacci numbers occur in the sums of "shallow" diagonals in Pascal's triangle (see Binomial coefficient).[18] The Fibonacci numbers can be found in different ways in the sequence of binary strings.
Relation to the golden ratioClosed-form expressionLike every sequence defined by a linear recurrence with constant coefficients, the Fibonacci numbers have a closed-form solution. It has become known as Binet's formula, even though it was already known by Abraham de Moivre:[19] where is the golden ratio (sequence A001622 in OEIS), and Since
Tthe] note that φ and ψ are both solutions of the equations so the powers of φ and ψ satisfy the Fibonacci recursion. In other words and
Combinatorial identitiesMo In particular, for all non-negative integers k. Some math puzzle-books present as curious the particular value which follows from the closed form for its partial sums as N tends to infinity: Primes and divisibilityDivisibility propertiesEvery 3rd number of the sequence is even and more generally, every kth number of the sequence is a multiple of Fk. Thus the Fibonacci sequence is an example of a divisibility sequence. In fact, the Fibonacci sequence satisfies the stronger divisibility property[32][33] This implies that any three consecutive Fibonacci numbers are pairwise coprime since
Fibonacci primesMain article: Fibonacci prime
A Fibonacci prime is a Fibonacci number that is prime. The first few are: Fibonacci primes with thousands of digits have been found, but it is not known whether there are infinitely many.[34] Fkn is divisible by Fn, so, apart from F4 = 3, any Fibonacci prime must have a prime index. As there are arbitrarily long runs of composite numbers, there are therefore also arbitrarily long runs of composite Fibonacci numbers. With the exceptions of 1, 8 and 144 (F1 = F2, F6 and F12) every Fibonacci number has a prime factor that is not a factor of any smaller Fibonacci number (Carmichael's theorem).[35] The only nontrivial square Fibonacci number is 144.[36] Attila Pethő proved in 2001 that there is only a finite number of perfect power Fibonacci numbers.[37] In 2006, Y. Bugeaud, M. Mignotte, and S. Siksek proved that 8 and 144 are the only such non-trivial perfect powers.[38] No Fibonacci number greater than F6 = 8 is one greater or one less than a prime number.[39] Prime divisors of Fibonacci numbersThe divisibility of Fibonacci numbers by a prime p is related to the Legendre symbol If p is a prime number then For example, It is not known whether there exists a prime p such that Such primes (if there are any) would be called Wall–Sun–Sun primes. Also, if p ≠ 5 is an odd prime number then:[41] Example 1. p = 7, in this case p ≡ 3 (mod 4) and we have: Example 2. p = 11, in this case p ≡ 3 (mod 4) and we have: Example 3. p = 13, in this case p ≡ 1 (mod 4) and we have: Example 4. p = 29, in this case p ≡ 1 (mod 4) and we have: For odd n, all odd prime divisors of Fn are congruent to 1 modulo 4, implying that all odd divisors of Fn (as the products of odd prime divisors) are congruent to 1 modulo 4.[42] For example, All known factors of Fibonacci numbers F(i) for all i < 50000 are collected at the relevant repositories.[43][44] Periodicity modulo nMain article: Pisano period
It may be seen that if the members of the Fibonacci sequence are taken mod n, the resulting sequence must be periodic with period at most n2−1. The lengths of the periods for various n form the so-called Pisano periods (sequence A001175 in OEIS). Determining the Pisano periods in general is an open problem,[citation needed] although for any particular n it can be solved as an instance of cycle detection. Right trianglesStarting with 5, every second Fibonacci number is the length of the hypotenuse of a right triangle with integer sides, or in other words, the largest number in a Pythagorean triple. The length of the longer leg of this triangle is equal to the sum of the three sides of the preceding triangle in this series of triangles, and the shorter leg is equal to the difference between the preceding bypassed Fibonacci number and the shorter leg of the preceding triangle. The first triangle in this series has sides of length 5, 4, and 3. Skipping 8, the next triangle has sides of length 13, 12 (5 + 4 + 3), and 5 (8 − 3). Skipping 21, the next triangle has sides of length 34, 30 (13 + 12 + 5), and 16 (21 − 5). This series continues indefinitely. The triangle sides a, b, c can be calculated directly: These formulas satisfy Any four consecutive Fibonacci numbers Fn, Fn+1, Fn+2 and Fn+3 can also be used to generate a Pythagorean triple in a different way:[45] Example 1: let the Fibonacci numbers be 1, 2, 3 and 5. Then: MagnitudeSince Fn is asymptotic to More generally, in the base b representation, the number of digits in Fn is asymptotic to Applications ApplicationsThe Fibonacci numbers are important in the computational run-time analysis of Euclid's algorithm to determine the greatest common divisor of two integers: the worst case input for this algorithm is a pair of consecutive Fibonacci numbers.[46] Yuri Matiyasevich was able to show that the Fibonacci numbers can be defined by a Diophantine equation, which led to his original solution of Hilbert's tenth problem. . This is known as Zeckendorf's theorem, and a sum of Fibonacci numbers that satisfies these conditions is called a Zeckendorf representation. The Zeckendorf representation of a number can be used to derive its Fibonacci coding.Fibonacci numbers are used by some pseudorandom number generators. Fibonacci numbers are used in a polyphase version of the merge sort algorithm in which an unsorted list is divided into two lists whose lengths correspond to sequential Fibonacci numbers – by dividing the list so that the two parts have lengths in the approximate proportion φ. A tape-drive implementation of the polyphase merge sort was described in The Art of Computer Programming. Fibonacci numbers arise in the analysis of the Fibonacci heap data structure. The Fibonacci cube is an undirected graph with a Fibonacci number of nodes that has been proposed as a network topology for parallel computing. A one-dimensional optimization method, called the Fibonacci search technique, uses Fibonacci numbers.[47] The Fibonacci number series is used for optional lossy compression in the IFF 8SVX audio file format used on Amiga computers. The number series compands the original audio wave similar to logarithmic methods such as µ-law.[48][49] Since the conversion factor 1.609344 for miles to kilometers is close to the golden ratio (denoted φ), the decomposition of distance in miles into a sum of Fibonacci numbers becomes nearly the kilometer sum when the Fibonacci numbers are replaced by their successors. This method amounts to a radix 2 number register in golden ratio base φ being shifted. To convert from kilometers to miles, shift the register down the Fibonacci sequence instead.[50] In natureYellow Chamomile
head showing the arrangement in 21 (blue) and 13 (aqua) spirals. Such
arrangements involving consecutive Fibonacci numbers appear in a wide
variety of plants.
Fibonacci sequences appear in biological settings,[8] in two consecutive Fibonacci numbers, such as branching in trees, arrangement of leaves on a stem, In addition, numerous poorly substantiated claims of Fibonacci numbers or golden sections in nature are found in popular sources, e.g., relating to the breeding of rabbits in Fibonacci's own unrealistic example, the seeds on a sunflower, the spirals of shells, and the curve of waves.[51] The Fibonacci numbers are also found in the family tree of honeybees.[52] The DNA molecule measures 34 angstroms long by 21 angstroms wide for each full cycle of its double helix spiral. 34 and 21, of course, are numbers in the Fibonacci series and their ratio, 1.6190476, closely approximates 1.6180339. A model for the pattern of florets in the head of a sunflower was proposed by H. Vogel in 1979.[54] This has the form where n is the index number of the floret and c is a constant scaling factor; the florets thus lie on Fermat's spiral. The divergence angle, approximately 137.51°, is the golden angle, dividing the circle in the golden ratio. Because this ratio is irrational, no floret has a neighbor at exactly the same angle from the center, so the florets pack efficiently. Because the rational approximations to the golden ratio are of the form F(j):F(j + 1), the nearest neighbors of floret number n are those at n ± F(j) for some index j, which depends on r, the distance from the center. It is often said that sunflowers and similar arrangements have 55 spirals in one direction and 89 in the other (or some other pair of adjacent Fibonacci numbers), but this is true only of one range of radii, typically the outermost and thus most conspicuous.[55] The bee ancestry codeFibonacci numbers also appear in the description of the reproduction
of a population of idealized honeybees,
If one traces the ancestry of any male bee (1 bee), he has 1 parent (1 bee), 2 grandparents, 3 great-grandparents, 5 great-great-grandparents, and so on. This sequence of numbers of parents is the Fibonacci sequence. The number of ancestors at each level, Fn, is the number of female ancestors, which is Fn−1, plus the number of male ancestors, which is Fn−2. ====================================================================== | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Total comments: 0 | |
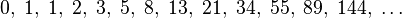 (sequence
(sequence 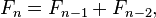
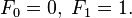




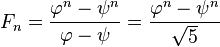
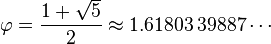

 , this formula can also be written as
, this formula can also be written as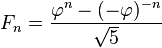






 .
.
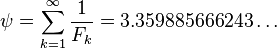



 which is evaluated as follows:
which is evaluated as follows:




















 for all n, but they only represent triangle sides when n > 2.
for all n, but they only represent triangle sides when n > 2.




 , the number of digits in Fn is asymptotic to
, the number of digits in Fn is asymptotic to  . As a consequence, for every integer d > 1 there are either 4 or 5 Fibonacci numbers with d decimal digits.
. As a consequence, for every integer d > 1 there are either 4 or 5 Fibonacci numbers with d decimal digits. .
.